2023. 1. 20. 21:49ㆍReinforcement Learning
Dynamic Programming (Model-based approach)
1. Prediction Problem (Policy evaluation)
- Treat Bellman equation like an update rule
- Could have just used a baisc linear solver but it doesn't scaled
- iterative DP approach applied
2. Control Problem (Policy improvement)
- Policy improvement theorem : If changing an action once improves the value, changing it every time will give us a better policy
- Policy iteration(slow)
- Value iteration (fast) : Almost like policy evaluation except take the max instead of sum
We already know the dynamics of the environment $p(s', r|s, a)$ which is called model-based approach
If we don't know the dynamics of the environment $p(s', r|s, a)$ we need to use model-free aproach
1. policy evaulation (prediction problem) (What is the value of a given policy?)

Since we know the dynamics of the environment, and discount factor is a constant, given a policy the value of states is the only variable in the equation(4.4). So we can solve it using linear algebra. (simultaneous linear equations in $|S|$ unknowns)
however it's computing costs will follow $O(n^3)$ so we need another approach.(Iterative approach)

But first we need to know if the following iteration method works. It's existence and uniqueness of $v_\pi$ are guaranteed as long as either $\gamma < 1$ or eventual termination is guaranteed from all states under the policy $\pi$
※ banach fixed-point theorem-proof for convergence
https://www.youtube.com/watch?v=9jL8iHw0ans
https://en.wikipedia.org/wiki/Banach_fixed-point_theorem

2. policy improvement (control problem) (What is the best policy?)
2-0) policy improvement theorem
The key criterion is whether one change of action $v_{\pi'}(s)$ is greater than or less than $v_\pi(s)$. If it is greater ----that is, if it is better to select a once in s and there after follow $\pi$ than it would be to follow $\pi$ all the time---- then one would expect it to be better still to select a every time $s$ is encountered, and that the new policy would in fact be a better one overall.
mathematical expression for policy improvement theorem

Then for all states $s \in S$:

proof for policy improvement theorem

So far we have seen how, given a policy and its value function, we can easily evaluate a change in the policy at a single state to a particular action. It is a natural extension to consider at all states and all possible actions, selecting at each state the action that appears best according to $q_\pi(s,a)$. In other words, to consider the new greedy policy, $\pi'$, given by

Suppose the new greedy policy, $\pi'$, is as good as, but not better than, the old policy $\pi$. Then $v_\pi = v_{\pi'}$, and from (4.9) it follows that for all $s \in S$:
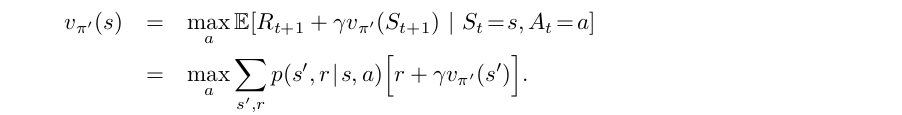
This guarantees that the policy is optimal policies and $v_{\pi'}$ must be $v_\star$
Policy Iteration and Value Iteration
2-1) Policy Iteration


2-2) Value Iteration
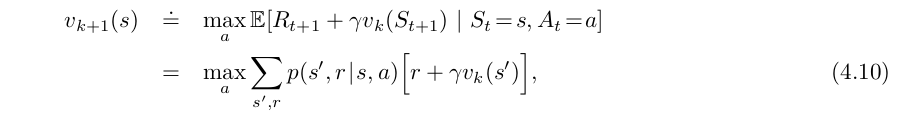

The problem with policy iteration is that there are two infinite loop in policy evaluation. We can improve this problem with value iteration. Just iterating value functions and after finding the optimal value function find the optimal policy for the given optimal values.
※ generalized policy iteration (GPI)

The term generalized policy iteration to refer to the general idea of letting policy-evaluation and policy-improvement
processes interact, independent of the granularity and other details of the two processes. Almost all reinforcement learning methods are well described as GPI. That is, all have identifiable policies and value functions, with the policy alwways being improved with respect to the value functio nand the value function always being driven toward the value function for the policy, as suggested by the diagram. If both the evaluation process and the improvement process stabilize, that is, no longer produce changes, then the value function and policy must be optimal. The value function stabilizes only when it is consistent with the current policy, and the policy stabilizes only when it is greedy with respect to the current value function. Thus, both processes stabilize only when a policy has been found that is greedy with respect to its own evaluation function. This implies that the Bellman optimality equation holds, and thus that the policy and the value function are optimal.
'Reinforcement Learning' 카테고리의 다른 글
| 5. Monte Carlo/ Temporal Difference (0) | 2023.01.31 |
|---|---|
| 3. Finite Markov Decision Processes (0) | 2023.01.13 |
| 2. Multi-Armed Bandits (0) | 2023.01.13 |
| 1. RL Introduction (0) | 2023.01.12 |